| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Stack
- 동적계획법
- 에라토스테네스의 체
- HashMap
- Dynamic Programming
- HashSet
- 반복문
- 메뉴리뉴얼
- 완전 탐색
- 영문자 확인
- 조합
- python
- 최소공배수
- 문자열
- fragment identifier
- 완전탐색
- 2017 카카오 코드
- 순열
- pandas
- Java
- 후위 표기법
- 보이어무어
- dfs
- 규칙찾기
- 프로그래머스
- 알고리즘
- 쿼드압축 후 개수세기
- 튜플
- 점프와 순간이동
- 어려웠던 문제
- Today
- Total
csmoon1010의 SW 블로그
자연어 처리 - 딥 러닝을 이용한 자연어 처리 입문(11) 본문
07. 머신러닝(Machine Learning) 개요
- AI = 머신 러닝 + 딥 러닝(머신 러닝의 한 갈래)
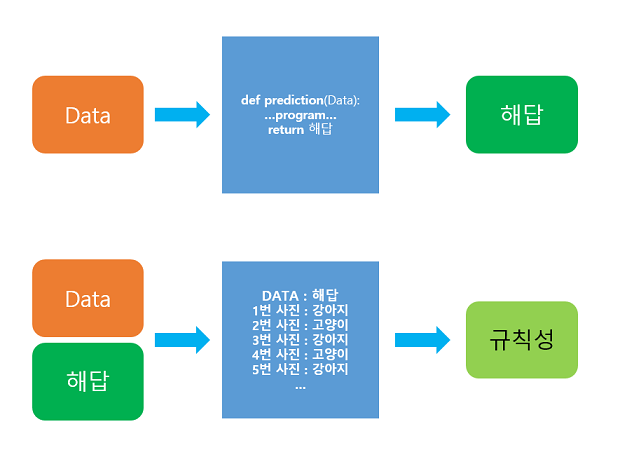
- 규칙을 찾아 프로그래밍 --> 스스로 규칙을 찾아감
- 활용분야 : 이미지 인식, 영상 처리, 알파고, 자연어 처리
- cf> 딥러닝 : 통계 기반보다 더 높은 성능을 보임
위키독스
온라인 책을 제작 공유하는 플랫폼 서비스
wikidocs.net
1) 머신 러닝이란(What is Machine Learning?)
1. 머신 러닝(Machine Learning)이 아닌 접근 방법의 한계
ex> 이미지 인식
사진 : 보는 각도, 조명, 타겟의 변형에 따라서 천차만별 --> "공통의 명확한 특징"을 잡아내기 어렵
--> 기존과 같은 명확한 알고리즘이 존재하지 않음.
2. 머신러닝은 기존 프로그래밍의 한계에 대한 해결책이 될 수 있다.
- 접근 방법, 초점 :
(1) 학습(training) = 주어진 데이터로부터 "규칙성"을 찾는다
(2) 새로운 데이터에 대해 발견한 규칙성을 기준으로 정답을 찾는다.
2) 머신 러닝 훑어보기
1. 머신 러닝 모델의 평가
(1) 데이터의 분리 : 훈련용, (검증용), 테스트용
- 검증용 데이터의 역할 : 모델의 성능을 조정하기 위한 용도 = 과적합 판단, 하이퍼파라미터의 조정
**하이퍼파라미터(초매개변수) : 값에 따라 "모델의 성능"에 영향을 주는 매개변수. 사용자가 직접 지정
ex> 선형회귀 - 경사하강법의 학습률(learning rate), 딥러닝 - 은닉층의 수, 뉴런의 수, 드롭아웃 비율
**매개변수 : 가중치, 편향과 같은 학습을 통해 바뀌어져가는 변수. 기계가 훈련을 통해서 바꾸는 변수
(2) 하이퍼파라미터의 "튜닝" : 검증용 데이터를 사용하여 정확도 검증하여 하이퍼파라미터 조정
(3) 모델 평가 : 테스트 데이터를 통해 모델의 성능을 평가한다.
**데이터가 충분하지 않음? : k-폴드 교차 검증
2. 분류(Classification)와 회귀(Regression)
- 분류 문제 : 로지스틱 회귀(Logistic Regression)
- 이진 분류(Binary Classification)
- 다중 클래스 분류(Multi-Class Classification)
- 다중 레이블 분류(Multi-lable Classification)
- 회귀 문제 : 선형 회귀(Linear Regression)
(1) 분류 _ 이진 분류 문제(Binary Classificaiton)
- 주어진 입력 --> 둘 중 하나의 답을 정하기
(2) 분류 _ 다중 클래스 분류(Multi-Class Classification)
- 주어진 입력 --> 두 개 이상 정해진 선택지 중 답을 정하기
- 범주/클래스 : 선택지
(3) 회귀 문제(Regression)
- 분류 문제처럼 비연속적인 답이 아닌 연속된 값을 결과로 가지는 문제
- ex> 시계열 데이터 --> 주가, 생산량, 지수 예측
3. 지도 학습(Suprevised Learning) & 비지도 학습(Unsupervised Learning)
- 지도 학습, 비지도 학습, 강화 학습으로 나뉘지만 여기선 강화학습은 다루지 않음
(1) 지도 학습
- "레이블(y, 실제값 = 정답)"과 함께 학습
- 학습 방식 : 예측값과 실제값 차이인 오차를 줄이는 방식
(2) 비지도 학습
- "레이블"이 없이 학습
- 예시 : LDA(토픽모델링), 워드투벡터(Word2Vec)
4. 샘플(Sample)과 특성(Feature)
- 보편적 문제 : 1개 이상의 독립변수 x --> 종속변수 y를 예측
- 보편적 연산 : 행렬 연산(독립변수, 종속변수, 가중치, 편향 등)
--> 훈련데이터를 "행렬"로 표현

- 샘플(Sample) : 하나의 데이터 = 행
- 특성(Feature) : 하나의 독립변수 = 열
5. 혼동 행렬(Confusion Matrix)
- 정확도(Accuracy) : (맞춘 문제수) / (전체 문제수)
- 혼동 행렬(Confusion Matrix) : 맞춘 결과, 틀린 결과에 대한 세부적인 내용을 알려줌
| 실제/예측 | 참 | 거짓 |
| 참 | TP | FN |
| 거짓 | FP | TN |
**True/False : 정답을 맞췄는가
**Positive/Negative : 제시했던 정답
(1) 정밀도(Precision)
양성을 양성으로 맞춘 경우(TP) / 양성이라고 대답한 전체 케이스(TP + FP)
(2) 재현률(Recall)
양성을 양성으로 맞춘 경우(TP) / 실제값이 양성인 케이스(TP + FN)
6. 과적합(Overfitting)과 과소 적합(Underfitting)
(1) 과적합(Overfitting) : 훈련 데이터를 과하게 학습한 경우(지나친 일반화)
--> 테스트 데이터, 실제 서비스 데이터에 대한 정확도는 떨어짐.
--> 훈련 데이터에 대한 오차↓BUT 테스트 데이터에 대한 오차↑

**테스트 데이터의 오차가 증가하기 전 OR 정확도가 감소하기 전에 적당한 epoch를 가져야
**막는 방법 : 드롭 아웃(Drop out), 조기 종료(Early Stopping)
(2) 과소 적합(Underfitting) : 성능이 더 올라갈 여지가 있음에도 훈련을 덜 할 상태
--> 훈련 데이터, 테스트 데이터에 대한 정확도 모두 낮음
3) 선형 회귀(Linear Regression)
1. 선형 회귀(Linear Regression)
- 독립 변수 x에 의해서 종속 변수 y의 값이 변함. --> 한 개 이상의 독립변수 x와 y의 선형 관계를 모델링
(1) 단순 선형 회귀 분석(Simple Linear Regression Analysis)
- 독립 변수의 개수가 1개인 회귀 분석식

- x : 독립 변수 / W : 가중치 / b : 편향(bias)
**W와 b를 적절히 찾아내어 x와 y의 관계를 적절히 모델링 한다.
(2) 다중 선형 회귀 분석(Multiple Linear Regression Analysis)
- 독립 변수의 개수가 여러개인 회귀 분석식 --> 여러개의 요소에 의해 결정되는 경우

2. 가설(Hypothesis) 세우기
- 단순 선형 회귀 문제
- 가설 : x와 y의 관계를 유추하기 위해 세워보는 수학적 식
H(x) = Wx + b
**직선의 기울기인 W와 y절편인 b에 따라 직선이 달라짐 --> 적절한 W와 b를 찾는게 중요!
3. 비용 함수(Cost function) : 평균 제곱 오차(MSE)
- 가설의 식에서 규칙을 가장 잘 표현하는 W와 b 찾기
- 목적 함수(Objective function) = 비용 함수(Cost function) = 손실 함수(Loss function) : 실제값과 예측값에 대한 오차에 대한 식
--> 함수의 값을 최소화/최대화 하는 "목적"을 가짐. 궁극적으로 "비용"과 "손실"을 최소화!!
- 평균 제곱 오차(Mean Squered Error, MSE) : 회귀문제에서 주로 사용되는 비용함수
- 오차(error) : 주어진 데이터에서 각 x에서의 실제값 y와 비용함수로 예측하고 있는 H(x)값의 차이(아래 그림의 ↕)

- 오차 크기 측정 방법
(1) 모두 더하기 : 양수 오차, 음수 오차가 모두 있으므로 이용 불가
(2) (오차 제곱)의 합
(3) 평균 제곱 오차(MSE) : (2)번의 평균(데이터 개수로 나눈다)
- 궁극적인 목표 : 평균 제곱 오차를 줄여 x와 y의 관계를 가장 잘 나타내는 직선을 그리자!!


4. 옵티마이저(Optimizer) : 경사하강법(Gradient Descent)
- 비용함수를 최소화하는 W, b를 찾기 위한 알고리즘
- 학습(training) : 옵티마이저를 통해 적절한 W, b를 찾아내는 과정
- 경사하강법(Gradient Descent) : 기본적인 옵티마이저 알고리즘
(1) W(가중치, 기울기)와 cost의 관계 : 너무 커지거나 작아질수록 cost값은 커진다.
--> 가장 최소인 그래프 상 볼록한 부분의 맨 아래 부분의 W를 찾아야!!
- 임의의 랜덤값 W
- 볼록한 부분을 향해 W값을 점차 수정(미분 : 접선의 기울기 = 0)
= 비용함수의 미분값이 0이 되는 곳을 향해 W의 값을 수정


**기울기가 양수이면 감소하는 방향으로 음수이면 증가하는 방향으로 조정되어 0인 방향으로 조정이 가능하다
**α : 학습률(learning rate) = W의 값을 변경할 때 얼마나 크게 변경할지
- 적당한 α값 : 높으면 W의 값이 발산, 낮으면 학습속도가 느림
(2) 실제 경사하강법 : W와 b에 대해서 동시에 경사하강법을 수행하여 최적의 W, b 찾기
5. 케라스로 구현하는 선형 회귀
- 케라스 모델의 기본적 형식
model = keras.models.Sequential() #Sequential로 모델 만들기
model.add(keras.layers.Dense(1, input_dim =1)) #필요 사항 추가 : 출력의 차원, 입력의 차원- 공부시간(x)와 성적(y)의 선형 회귀


4) 로지스틱 회귀(Logistic Regression) - 이진 분류
- 로지스틱 회귀 : 둘 중 하나를 결정하는 문제인 이진분류를 풀기 위한 대표적인 알고리즘
1. 이진 분류(Binary Classification)
- 선형 회귀처럼 직선 그래프로 나타내기 적합하지 않음
- 예측값을 두가지 값 중에 하나를 가지도록 하는것이 보편적 (ex> 0과 1 중 하나 : 예측값 > 0.5 --> 1)
--> 시그모이드 함수이용
2. 시그모이드 함수(Sigmoid function)
- 시그모이드 함수 방정식=가설식

- 시그모이드 함수 그래프 : 0일 때 0.5, x가 증가하면 1에 수렴, x가 감소하면 0에 수렴

- 가중치 W : 그래프의 경사도를 결정(W가 커질수록 경사가 커진다)

- 편향 b : 그래프가 위, 아래로 이동

3. 비용 함수(Cost function)
- 경사 하강법 이용 but 평균 제곱 오차 이용안함!
- 평균제곱오차 이용 안하는 이유 : 글로벌 미니멈이 아닌 로컬 미니멈에 도달할 가능성이 있음.

- 시그모이드 함수에서 이용할 비용 함수 구하기
: 로그 함수를 이용하여 나타냄.

**실제값이 1 : 예측값이 0이면 오차가 1 --- 오차 감소 --- 예측값이 1이면 오차가 0
**실제값이 0 : 예측값이 0이면 오차가 0 --- 오차 증가 --- 예측값이 1이면 오차가 1

- 크로스 엔트로피(Cross Entropy) : 두 경우를 하나의 식으로 표현하여 만든 비용함수
--> 최종 목적 함수 = 크로스 엔트로피 함수의 평균을 취한 함수

4. 케라스로 구현하는 로지스틱 회귀
- 로지스틱 회귀 모델 생성

- 크로스 엔트로피 그래프 생성

- 값 추정

'데이터&인공지능 > 자연어처리' 카테고리의 다른 글
| 자연어 처리 - 딥 러닝을 이용한 자연어 처리 입문(13) _ 딥러닝 (0) | 2020.02.21 |
|---|---|
| 자연어 처리 - 딥 러닝을 이용한 자연어 처리 입문(12) (0) | 2020.02.18 |
| 자연어 처리 - 딥 러닝을 이용한 자연어 처리 입문(10) (0) | 2020.02.16 |
| 자연어 처리 - 딥 러닝을 이용한 자연어 처리 입문(9) (0) | 2020.02.15 |
| 자연어 처리 - 딥 러닝을 이용한 자연어 처리 입문(8) (0) | 2020.02.15 |




